NOTE: this post has three basic problems. It assumes property 1 and 2 are true, and there is a missing piece at the end that keeps us from showing anything :)
This post results from a bunch of conversations with Dave Hart and the twitter hive brain. There are several ways to generate a random Lambertian direction from a point with surface normal N. One way is inspired by a cool paper by Sbert and Sandez where he simultaniously generated many form factors by repeatedly selecting a uniformly random 3D line in the scene. This can be used to generate a direction with a cosine density, an idea first described, as far as I know, by Edd Biddulph.
I am going to describe it here using three properties, each of which I don't have a concise proof for. Any help appreciated! (I have algebraic proofs-- they just aren't enlightening--- hoping for a clever geometric observation).
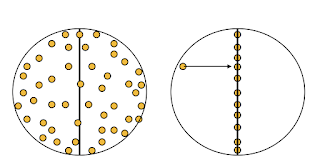
Property 1: Nusselt Analog: uniform random points on an equatorial disk projected onto the sphere have a cosine density. So in the figure, the red points, if all of them projected, have a cosine density.
Property 2: (THIS PROPERTY IS NOT TRUE-- SEE COMMENTS) The red points in the diagram above when projected onto the normal, will have a uniform density along it:
Property 3: For random points on a 3D sphere, as shown (badly) below, they when projected onto the central axis will be uniform on the central axis.Now if we accept Property 3, we can first generate a random point on a sphere by first choosing a random phi uniformly theta = 2*PI*urandom(), and then choose a random height from negative 1 to 1, height = -1 + 2*urandom()
In XYZ coordinates we can convert this to:
z = -1 + 2*urandom()
phi = 2*PI*urandom()
x = cos(phi)*sqrt(1-z*z)
y = sin(phi)*sqrt(1-z^2)
Similarly from property 2 we can given a random point (x,y) on a unit disk in the XY plane, we can generate a direction with cosine density when N = the z axis:
(x,y) = random on disk
z = sqrt(1-x*x-y*y)
To generate a cosine direction relative to a surface normal N, people usually construct a local basis, ANY local basis, with tangent and bitangent vectors B and T and change coordinate frames:
get_tangents(B,T,N)
(x,y) = random on disk
z = sqrt(1-x*x-y*y)
direction = x*B + y*T + z*N
There is finally a compact and robust way to write get_tangents. So use that, and your code is fast and good.
But can we do this show that using a uniform random sphere lets us do this without tangents?
So we do this:
P = (x,y,z) = random_on_unit_sphere
D = unit_vector(N + P)
So D is the green dot while (N+P) is the red dot:
So is there a clever observation that the green dot is either 1) uniform along N, or 2, uniform on the disk when projected?



5 comments:
Property 3 is correct. Property 2 is an incorrect restatement of it. In-particular, as to your final figure, the red dot is uniformly distributed when projected onto N, but the green dot is not.
Yeah Ian's right, the cosine weighted hemisphere samples aren't uniform in z. I think hemisphere z values are linearly distributed from 0 density at the base to a maximum at the apex.
Property 1 has to be true though, the green dot has to be uniform when projected to the disk.
I was just playing with it a little and noticed something that wasn't obvious to me, but might be already obvious to you guys.
If you sample a sphere of radius 0.5 with center (0, 0, 0.5), then project it to the hemisphere of radius 1: the length of the vector from the origin to the sphere sample is equal to the z value of the hemisphere sample. That suggests that we might find some geometric intuition by looking at the smaller hemisphere passing through the sphere sample. Maybe?
It is certainly an interesting observation, at least to me. The proof is straightforward, but only in retrospect:
https://i.imgur.com/vv8NrBL.png
Starting from a unit (hemi)circle at origin A, we draw radii AD and AE separated by angle DAE = θ < 90°. We then drop a perpendicular from D to AE to get B. Bisecting AE and drawing a circle from the bisected point to A or E, take its intersection with AD to be C. The claim is that AB = AC.
To see this, simply draw line CE. Observe that angle ACE is an inscribed angle of a hemicircle (the smaller circle). Therefore, by a well-known theorem, it is 90°. Considering right triangles ABD and ACE, we see that AB and AC must both be cos(θ), and are therefore equal.
An interesting article and proposed solutions. I agree with the authors of previous posts and thank you for thewww.fastcustomwritinghelp.com/blog/customer-satisfaction-is-a-must points of view and the proposed solutions. Informatively.
Post a Comment